Notes on Analytical Mechanics
Discussing the roots of Analytical Mechanics and its Impact on Quantum Mechanics
On the morning of Saturday, before grabbing my first cup of coffee for the day, I found myself deep-diving into Lagrangian points. There was no specific reason, no urgent project demanding my attention in that area, just pure, undirected curiosity. It’s one of those moments where you catch yourself nerding out over something so niche, you can't help but wonder how you even got there. But there I was, absorbed in celestial mechanics.
That’s when the idea for this article hit me - the sheer scale of impact analytical mechanics has had on physics as we know it.
I've spent a good chunk of my career in the trenches of engineering and science, always with a bias towards understanding the mechanics of things. Not just how they work, but why they work the way they do.
Newton's laws have been the bedrock of classical mechanics, sure. They've given us the tools to predict the movement of objects under various forces, and that's been invaluable. But, if I'm being honest, there’s always been this gap between the straightforward applications of Newton’s laws and the complex, often chaotic reality of how celestial bodies move and interact.
That’s where analytical mechanics, and specifically the work of Joseph-Louis Lagrange, comes into play. Lagrange didn’t just take Newton's playbook and run with it; he pretty much rewrote the rules of the game. By shifting the focus from vectors of force to the scalar quantities of energy and potential, analytical mechanics provided a new lens to view and solve physical problems.
Reflecting on Lagrangian points that morning made me appreciate this shift even more. These points are a perfect case study of analytical mechanics in action, applying Newtonian principles in ways that were previously unimaginable. This rabbit hole of thought led me to consider other facets of analytical mechanics, like the principle of least action, its knack for generalisation and abstraction, and its groundbreaking role in paving the way for quantum mechanics.
So I thought of sharing some notes on what I learned over my unexpected morning read. If you're into the nuts and bolts of how the universe ticks, this one's for you. Let’s get started!
The Limitations of Newtonian Mechanics
Sir Isaac Newton's work laid down the foundations of classical mechanics, encapsulating the motion of bodies under the influence of forces through three laws. While groundbreaking, this framework presents challenges when applied to complex systems, particularly in the realm of celestial mechanics.
Newton's Second Law, , where represents the net force applied to an object, its mass, and acceleration is crucial to classical mechanics. However, the application of this law assumes a straightforward, deterministic view of motion, which becomes increasingly cumbersome when dealing with systems subjected to multiple forces, especially in non-inertial frames of reference.
Moreover, the abstraction of forces in Newton's formulation does not readily lend itself to systems where energy, rather than forces per se, is more transparent and pivotal to understanding the system's dynamics.
This is particularly evident in celestial mechanics, where the motion of bodies is influenced by the gravitational pull from multiple celestial entities, leading to complex, non-linear paths that are not easily deduced from Newton’s laws alone.
Bridging the Gap with Analytical Mechanics
Lagrange's formulation, encapsulated in the Lagrangian function , where represents the kinetic energy and the potential energy of the system, shifts the focus from forces to the scalar quantities of energy. This transition from vectors to scalars is a fundamental shift in perspective that allows for a more generalised and flexible approach to dynamics.
The elegance of the Lagrangian formulation lies in its capacity to abstract and simplify the equations of motion for complex systems, including those with constraints, through the principle of least action.
This principle posits that the path taken by a system between two points is the one for which the action integral, , is stationary (typically, a minimum). This approach does not merely solve for motion; it reveals the underlying geometrical and energetic symmetries of the physical laws governing the system.
By applying the Lagrangian framework to the realm of celestial mechanics, one can derive the equations of motion for bodies in space without direct recourse to the vectorial forces acting upon them. This methodology provides deeper insights into the nature of the forces at play, including the gravitational interactions that define the motion of celestial bodies.
The Lagrangian Points
Before moving forward, it is ideal to clarify what Lagrangian points are. In the simplest of terms, these points represent positions in space where the gravitational forces of two large bodies, such as the Earth and the Moon, balance the centrifugal force felt by a smaller object. The mathematical derivation of these points, and the understanding of their stability, is made possible through the Lagrangian framework.
The Paradigm Shift from Vectors to Scalars
As discussed above, the limitations of Newtonian mechanics, when applied to complex systems, were circumvented by Analytical mechanics. The key idea that made the difference was a shift in perspective by considering energy states using scalars instead of vectors. So before we discuss the Principle of Least Action, I think it would be ideal to discuss this paradigm shift in detail, so we have a better understanding of its impact on modern day physics.
In classical Newtonian mechanics, the analysis of a system’s behaviour is predominantly focused on the forces acting upon objects and their resultant accelerations. This approach becomes increasingly complex and unwieldy when applied to systems with numerous interacting parts or those subject to non-conservative forces. The vectorial nature of forces necessitates a detailed, direction-based analysis, which can obscure the underlying symmetries and conservation laws that are pivotal to understanding the system's dynamics.
Analytical mechanics introduced a scalar-based approach using the Lagrangian function. This transition to a scalar framework simplified the representation of a system's state, reducing the complexity of the equations of motion through the Euler-Lagrange equation:
where are the generalised coordinates representing the system’s configuration, and their time derivatives. This equation captures the dynamics of a wide variety of systems in a form that highlights the conservation of energy and other fundamental physical properties.
The Hamiltonian formulation furthers this scalar approach by introducing the Hamiltonian function, , which is often equivalent to the total energy of the system. The Hamiltonian is a tool for analysing systems, especially in quantum mechanics, where it plays a central role.
The Principle of Least Action
Okay, now let’s talk about the Principle of Least Action which is a powerful unifying principle across various domains of classical and modern physics. This principle states that the path taken by any system between two points is not arbitrary but is one that minimises the action, a quantity defined as the integral of the Lagrangian over time.
Mathematically, the action, , is expressed as:
where represents the Lagrangian of the system, with denoting kinetic energy and potential energy, and and the initial and final times over which the action is evaluated. The principle asserts that the actual path taken by the system makes the action stationary (typically, a minimum).
The Euler-Lagrange equation is a direct outcome of applying the principle of least action to determine the equations of motion for a system.
Generalisation and Abstraction in Analytical Mechanics
Now that we understand the principle of least action, we can talk a bit about the power of generalisation and abstraction in analytical mechanics. After all, the principle of least action is an excellent example of the power of generalisation and abstraction inherent in analytical mechanics.
By focusing on the scalar quantities of action, energy, and potential, this framework transcends the specifics of the forces at play, providing a more generalised and elegant description of physical phenomena. This abstraction facilitates a deeper understanding of the underlying symmetries and conservation laws, which are often obscured in a more direct, force-based analysis.
The beauty of this principle lies in its applicability across a wide range of physical contexts, from the motion of particles in a potential field to the dynamics of fields themselves in the realm of field theory.
Interestingly, this also makes it a bridge between classical mechanics and quantum mechanics, where the action plays a pivotal role in the path integral formulation of quantum mechanics. So, let us now talk about how this all adds up together with quantum mechanics.
Impact on Quantum Mechanics
The methodologies and concepts developed by Lagrange, Hamilton, and others have provided the essential tools and perspectives necessary to explore and formalise the quantum realm (to the best extent possible).
Hamiltonians and Quantum States
The Hamiltonian function, representing the total energy of a system, translates into the Hamiltonian operator in quantum mechanics. This operator plays a key role in the Schrödinger equation,
where is the Hamiltonian operator, the wave function of the quantum system, the imaginary unit, and the reduced Planck's constant. This equation governs the evolution of quantum states, directly linking the abstract energy-centric perspective of analytical mechanics with the probabilistic nature of quantum phenomena.
Principle of Least Action and Path Integral Formulation
The principle of least action extends its influence to quantum mechanics through the path integral formulation. Developed by Richard Feynman, this formulation conceptualises the behaviour of particles not as a single, deterministic path but as a sum over all possible paths, each weighted by an exponential factor related to the action,
Here, represents the action of a particular path, and denotes integration over all possible paths. This revolutionary approach has provided deep insights into the quantum behaviour of particles. It also underscored the unifying principles of physics across different scales and regimes.
Analytical Mechanics and Quantum Field Theory
The abstraction and generalisation inherent in analytical mechanics paved the way for the development of Quantum Field Theory (QFT), the theoretical framework combining quantum mechanics with special relativity to describe particle physics.
The Hamiltonian and Lagrangian formulations provide the mathematical structure for QFT, where fields are treated as dynamical entities governed by similar principles as those in classical mechanics, but within the quantum context. This has led to insights into the fundamental forces of nature and the particles that constitute the universe.
Analytical Mechanics is a Force for Unification and Discovery
The impact of analytical mechanics on quantum mechanics and, by extension, on the entirety of modern physics, is immense! By offering a unified, abstract framework for understanding the dynamics of physical systems, analytical mechanics has not only bridged the gap between classical and quantum physics to the best extent possible, but has also laid the foundational principles for future discoveries. Its legacy is one of unification and discovery that, in a poetic sense, makes it a great example for the power of abstract thought in uncovering the mysteries of the universe.
When we speak of classical physics, we speak of Newton and rightfully so. When we speak of quantum physics, we speak of Schrödinger, Einstein, and Feynman and rightfully so. But often what we forget, is the role of Lagrange, Euler and Hamilton, in connecting the dots and building the tools necessary to unify these theories from seemingly disparate fields to the best extent possible. I hope this article helped in underlining this point.




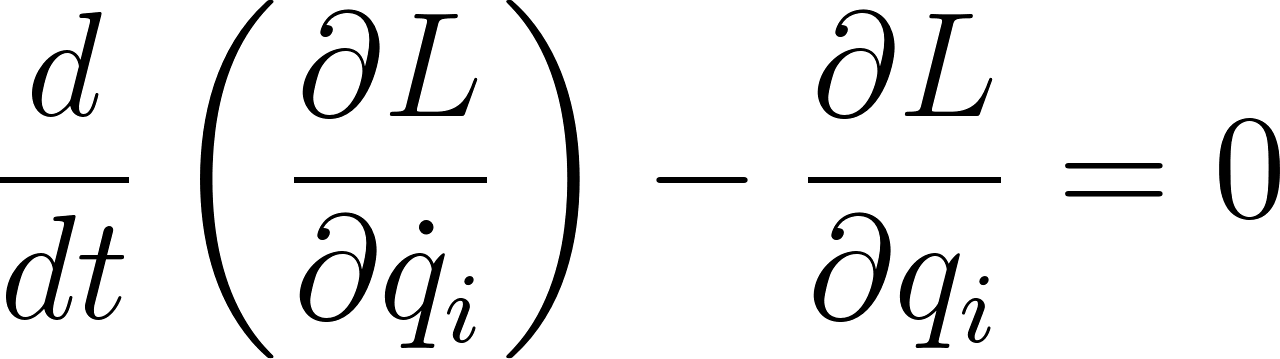

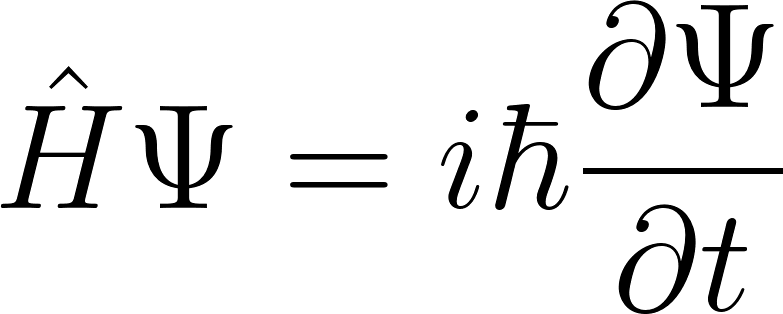

Nice article, very engaging. Already thinking about how to integrate what I'm studying with what you wrote. I am currently studying the implications of quantum field theory. Matching with your reflections on the limits of Newton's deterministic theories: How does gravitational pull change instantaneously throughout the universe?
Thanks for your piece, I will have a look at it along with my notes :-)